Read Time: 10 min

---

So, you’re gonna have a rad kickback at your place and wanna invite your friends Abby, Becky, Carl, Dan, Elise, and Francine.

But ….

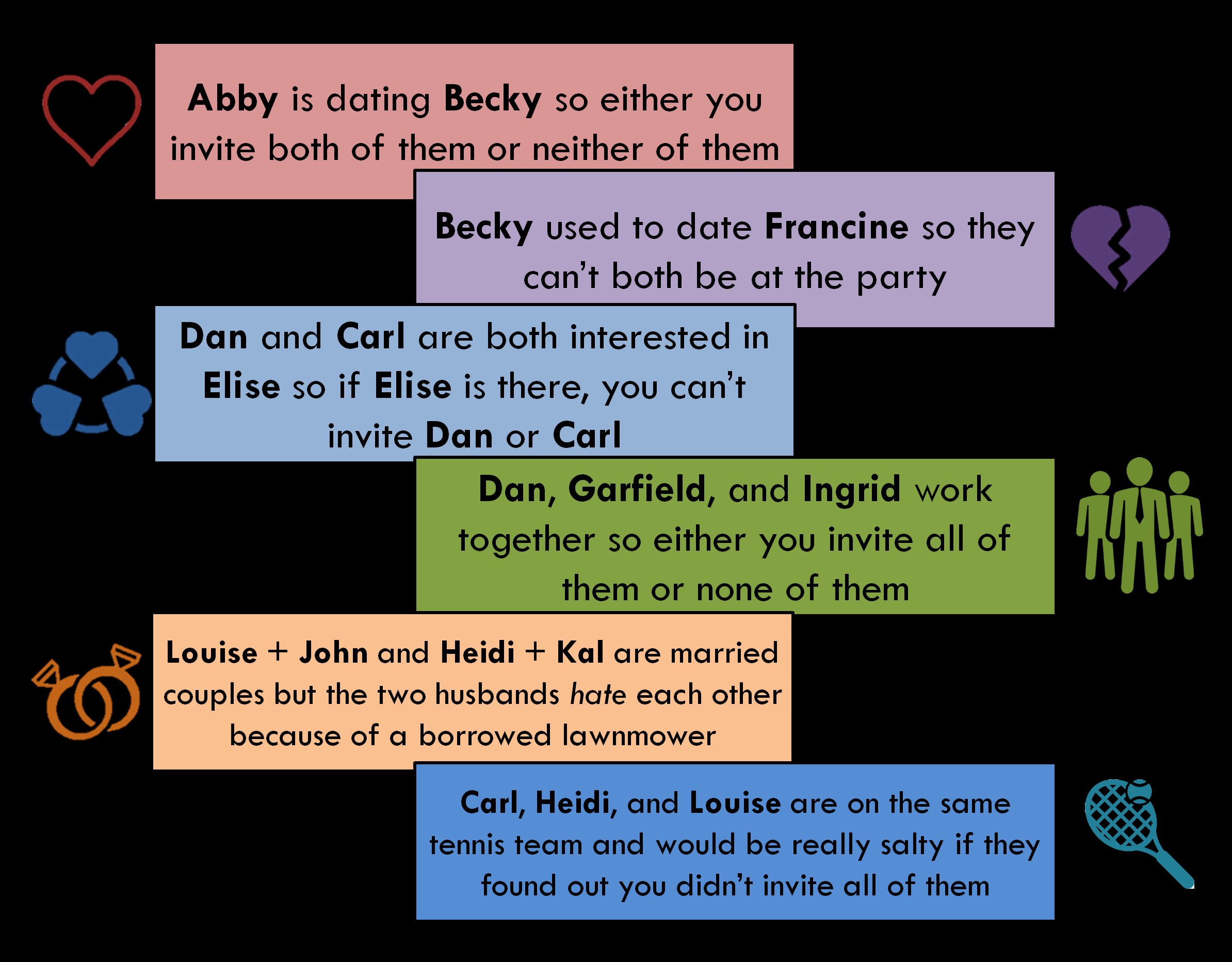
If you’re inviting Abby, you have to invite Becky because they’re dating and it would look sooo shady if you just invited one of them.

Alsooo if Becky’s gonna be there, then you absolutely cannot invite Francine because they used to date and it did not end well.

Oh yea, and Carl and Dan are both trying to get with Elise so if Elise is coming, then there’s no way that Dan or Carl can be there.

Also, you sit down and score how much you want each person at your party and come up with this list:

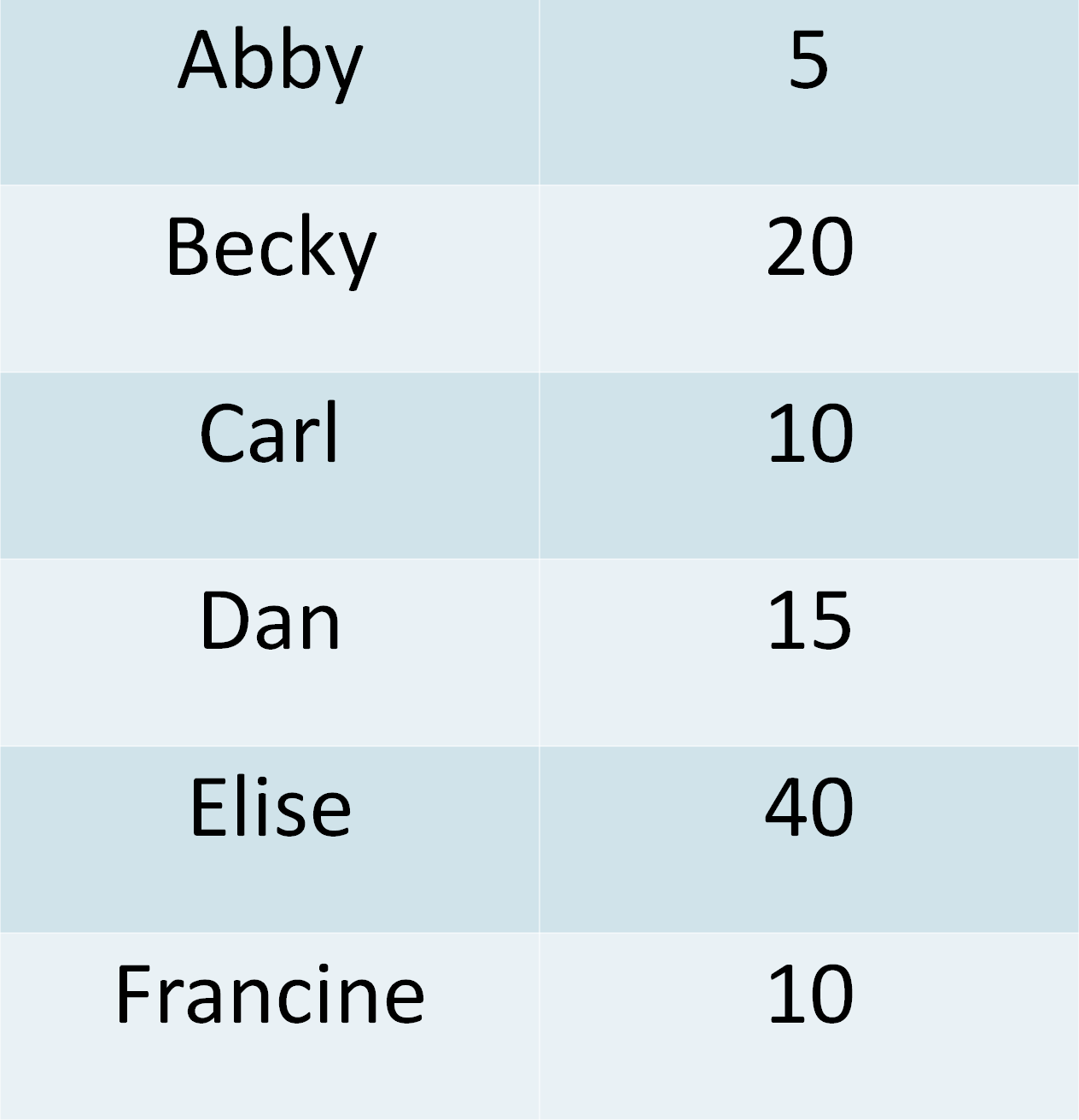
Who ends up getting an invite to your party?

Well, since this is a pretty simple case, we can just logic it out here.

Let’s say we invite Abby. Then we have to also invite Becky. Also, then we cannot invite Francine. So it’s either Abby + Becky or Francine. Abby + Becky gives us 25 points while Francine gives us just 10. Too bad for Francine … bye Felicia. Abby and Becky are in.

Also, let’s say we invite Carl and Dan. Then Elise cannot be there. Vice versa, we can invite Elise but then we cannot invite Carl or Dan. Carl + Dan gives us 25 and Elise gives us 40. So Elise gets an invite.

So, our final guest list is Abby, Becky, and Elise, for a total of 65 points out of a possible 100. Not Bad!!

But what if it’s more complicated. Consider a bunch of amigos and the following restrictions:

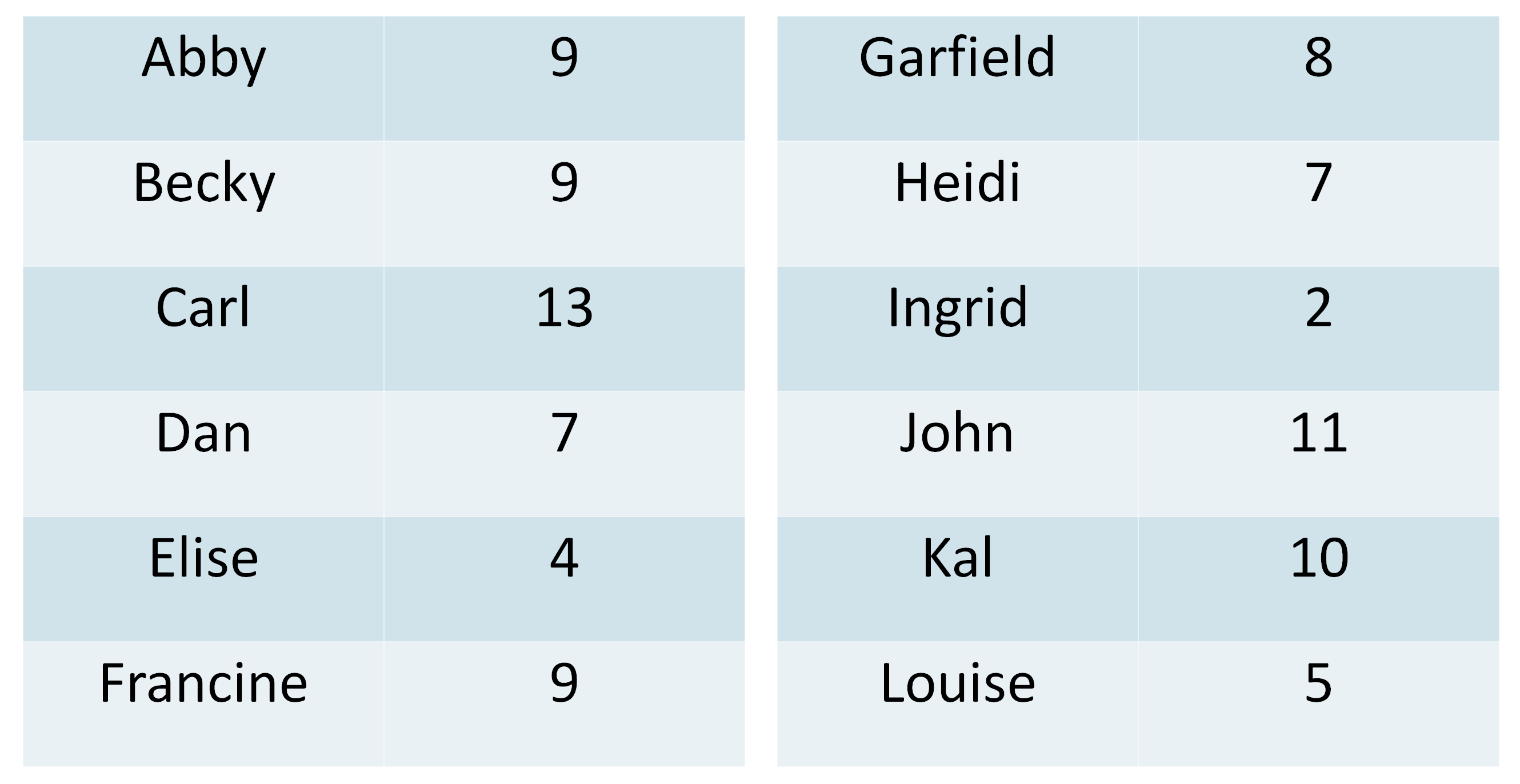
Also, this is our points list for all our friends:

Now what do we do??

We can use a powerful mathematical solving technique called Linear Programming to solve this problem.

First, we set up the problem by having a bunch of binary (0 or 1) variables, each corresponding to one of our potential guests. For example, in Abby’s case:

\[A = \left\{ \begin{array}{ll} 1 & \text{if Abby is coming to the party} \\ 0 & \text{if not} \\ \end{array} \right .\]

and all other variables are defined similarly.

So how do we say mathematically that Becky and Francine can’t both be at the party?

Well, it’s fine if Becky is there without Francine \((B=1, F=0)\) or if Francine is there without Becky \((B=0, F=1)\). It’s also fine if neither is there \((B=0, F=0)\). So basically, we need that \(B+F \leq 1\) since the only unacceptable case is if both of them are there \((B=1,F=1 \to B+F=2)\).

How about if some people have to be at the party together? If Abby and Becky have to be at the party together, then either \(A=0,B=0 \to A+B=0\) or \(A=1,B=1 \to A+B=2\). (See the notes for discussion on how to encode this as a set of constraints compatible with Linear Programming).

We can also get a bit fancier. For example if we can either invite one couple (Louise and John) or another couple (Kal and Heidi) (because of the lawnmower snafu), then we can encode that as: \((L+J) + (K+H) \leq 2\) (this works because \(L+J\) is either \(0\) or \(2\) and same with \(K+H\), so this constraint ensures that \(L+J\) and \(K+H\) are not both \(2\)).

Putting all our constraints into our Linear Programming model, along with our preference points for the potential guests, we quickly generate the optimal drama-free guest list:

Let’s do a quick check to make sure we can’t do better. The highest scoring person, Carl with 13 points, didn’t get an invite! But if he did, then we have to invite Heidi and Louise too because of the tennis team constraint. But then we have DRAMA because we invited Heidi and Louise, whose husbands hate each other. Don’t wanna get caught up in that mess!

So … yea. Let’s be honest. There’s just some people who can’t be around other people at your kickback, bat mitzvah, wedding, etc. And you don’t wanna deal with all that drama so just let the math take care if it for you. :)

Thanks for reading and please leave comments!

Notes

---

For those familiar with the procedure of Linear Programming, you know that we are only allowed to combine our constraints using AND, i.e. we can say \(x + y \leq 4\) AND \(x - y \geq 3\) AND etc.

The constraint we mentioned in this post about making sure two people either attend a party together or not at all is actually an OR constraint. i.e. something like \(x = 0\) OR \(x = 2\). We can use something called the Big M method to convert this or constraint into a group of OR constraints. Namely, we convert the constraint \(x = 0\) OR \(x = 2\) into:

\[x \geq 0 \\ x - M \times z_1 \leq 0 \\ x + M \times z_2 \geq 2 \\ z1 + z2 = 1\]

where we have introduced two new variables, \(z_1\) and \(z_2\), which are both binary variables and which add up to 1. We have also introduced a constant called M which is very large. We will set it to be 100.

Note that the only two possible cases are \((z_1, z_2) = (0, 1)\) or \((z_1, z_2) = (1, 0)\). In the former case, our constraints reduce to:

\[x \geq 0 \\ x \leq 0 \\ x \geq -98\]

which all just reduces to \(x = 0\).

In the latter case, our constraints reduce to:

\[x \geq 0 \\ x \leq 100 \\ x \geq 2\]

which reduces to

\[2 \leq x \leq 100\]

In our case, x is actually the sum of the two binary variables representing the two people we need at the party together and so it all reduces to \(x = 2\).

Thus, by introducing an extra set of variables, \(z_1\) and \(z_2\), we are able to capture our OR constraint.